Simulate Joint ODE Model Data

Generates synthetic data from a sophisticated joint modeling framework that seamlessly integrates longitudinal biomarker trajectories with survival outcomes through ordinary differential equations (ODEs). This simulation engine produces realistic clinical trial datasets where complex biomarker dynamics govern event hazards via shared random effects and trajectory features, capturing the intricate interplay between disease progression and time-to-event processes.

Usage

simulate(
  n = 50,
  alpha = c(0.5, 0.4, -0.5),
  beta = c(-0.3, -0.5, 0.2, 0.1, 0.05),
  phi = c(0.2, -0.15),
  weibull_shape = 1.5,
  weibull_scale = 8,
  sigma_b = 0.1,
  sigma_e = 0.1,
  seed = 42,
  verbose = TRUE
)

Arguments

n: Integer. Number of subjects to simulate. Larger cohorts provide more stable parameter estimates (default: 50).
alpha: Numeric vector of length 3. Association parameters quantifying how trajectory features influence survival hazard: [biomarker, velocity, acceleration]. Positive values indicate increased risk (default: c(0.5, 0.4, -0.5)).
beta: Numeric vector governing ODE dynamics (length 5). Controls biomarker trajectory evolution: [biomarker, velocity, x1, x2, time]. Automatically normalized to unit length for identifiability (default: c(-0.3, -0.5, 0.2, 0.1, 0.05)).
phi: Numeric vector of length 2. Baseline covariate effects modulating survival hazard independently of biomarker dynamics: [w1, w2] (default: c(0.2, -0.15)).
weibull_shape: Numeric. Weibull shape parameter ($\kappa$) characterizing baseline hazard evolution. Values > 1 yield increasing hazard (aging effect), < 1 decreasing hazard (selection effect), = 1 constant hazard (exponential) (default: 1.5).
weibull_scale: Numeric. Weibull scale parameter ($\theta$) determining the characteristic event time. Larger values shift the hazard curve rightward (default: 8).
sigma_b: Numeric. Standard deviation of subject-specific random effects capturing unobserved heterogeneity. Larger values increase between-subject variability in both trajectories and hazards (default: 0.1).
sigma_e: Numeric. Measurement error standard deviation reflecting assay precision and biological fluctuations. Smaller values indicate more reliable biomarker measurements (default: 0.1).
seed: Integer. Random seed ensuring reproducible simulations. Essential for method validation and comparison studies (default: 42).
verbose: Logical. Display informative progress messages during simulation workflow (default: TRUE).

Value

A list containing two complementary datasets:

longitudinal_data

Data frame with longitudinal measurements:

id: Subject identifier
time: Measurement time
v: Observed biomarker value incorporating latent trajectory, random effect, and measurement error
x1: First longitudinal covariate (standardized)
x2: Second longitudinal covariate (standardized)
biomarker: True latent biomarker trajectory value
velocity: True latent biomarker velocity value
acceleration: True latent biomarker acceleration value

survival_data

Data frame with survival outcomes:

id: Subject identifier
time: Observed event/censoring time
status: Event indicator (1 = event, 0 = censored)
w1: First survival covariate (standardized)
w2: Second survival covariate (standardized)
b: Shared random effect

Details

Mathematical Framework

The simulation orchestrates a sophisticated joint model architecture comprising two intricately coupled components:

1. Longitudinal Dynamics

Biomarker evolution is governed by a second-order nonlinear ODE system that captures complex temporal dynamics: $$\ddot{m}_i(t) = g(\boldsymbol{\beta}^{\top} \mathbf{Z}_i(t))$$

where:

$m_i(t)$: Latent biomarker trajectory for subject $i$
$\mathbf{Z}_i(t) = [m_i(t), \dot{m}_i(t), X_1, X_2, t]^{\top}$: State vector (5-dimensional)
$g(u) = 2 \tanh(u/3)$: Bounded nonlinear transformation ensuring numerical stability and biological plausibility
$\boldsymbol{\beta}$: Parameter vector governing homeostatic feedback, damping forces, and external influences

Observed measurements arise from a hierarchical structure incorporating both systematic and stochastic components: $$V_{ij} = m_i(T_{ij}) + b_i + \varepsilon_{ij}$$

where $b_i \sim N(0, \sigma_b^2)$ captures subject-specific deviations and $\varepsilon_{ij} \sim N(0, \sigma_e^2)$ represents measurement variability.

2. Survival Process

The instantaneous hazard function elegantly links biomarker dynamics to event risk through a multiplicative model: $$\lambda_i(t|b_i) = \lambda_0(t) \exp[\boldsymbol{\alpha}^{\top} \mathbf{m}_i(t) + \mathbf{W}_i^{\top} \boldsymbol{\phi} + b_i]$$

where:

$\lambda_0(t) = (\kappa/\theta)(t/\theta)^{\kappa-1}$: Weibull baseline hazard capturing population-level risk evolution
$\mathbf{m}_i(t) = [m_i(t), \dot{m}_i(t), \ddot{m}_i(t)]^{\top}$: Comprehensive trajectory feature vector
$\mathbf{W}_i$: Time-invariant baseline characteristics
$b_i$: Shared random effect inducing correlation between longitudinal and survival processes

Simulation Workflow

The data generation proceeds through a carefully orchestrated pipeline:

ODE Integration: Numerical solution of the coupled ODE system using adaptive Runge-Kutta methods with automatic step size control for optimal accuracy-efficiency tradeoff
Event Time Generation: Sophisticated sampling from the conditional hazard distribution via the simsurv engine, accounting for complex time-varying covariates
Censoring Mechanism: Realistic administrative censoring uniformly distributed between the 50th and 95th percentiles of event times, mimicking clinical trial follow-up patterns
Visit Scheduling: Adaptive measurement protocols with higher frequency during critical periods (quarterly initially, semi-annual subsequently) and stochastic 10% missingness

Parameter Interpretation Guide

Trajectory Dynamics (beta):
- beta[1]: Homeostatic feedback strength (negative values promote stability)
- beta[2]: Damping coefficient controlling oscillation suppression
- beta[3-4]: Sensitivity to longitudinal covariates
- beta[5]: Time trend capturing systematic changes
Hazard Association (alpha):
- alpha[1]: Current biomarker value effect (positive indicates deleterious biomarker)
- alpha[2]: Velocity effect capturing prognostic value of trajectory direction
- alpha[3]: Acceleration effect reflecting stability importance (negative suggests protective stability)

Note

Parameter vector beta undergoes automatic normalization to unit length, ensuring model identifiability without user intervention
Visit schedules intelligently adapt to individual follow-up durations, balancing information gain with practical constraints
Progress reporting can be silenced via verbose = FALSE for batch simulations

Examples

# Basic usage with default parameters
sim <- simulate()
#> Step 1/2: Generating survival times...
#> Step 2/2: Generating longitudinal data...
str(sim)
#> List of 2
#>  $ longitudinal_data:'data.frame':	747 obs. of  8 variables:
#>   ..$ id          : int [1:747] 1 1 1 1 1 1 1 1 1 1 ...
#>   ..$ time        : num [1:747] 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.5 ...
#>   ..$ v           : num [1:747] 0.1872 0.1778 0.1431 0.0385 -0.2236 ...
#>   ..$ x1          : num [1:747] -0.0407 -0.0407 -0.0407 -0.0407 -0.0407 ...
#>   ..$ x2          : num [1:747] -2 -2 -2 -2 -2 ...
#>   ..$ biomarker   : num [1:747] 0 -0.00646 -0.02413 -0.05051 -0.08327 ...
#>   ..$ velocity    : num [1:747] 0 -0.05 -0.0897 -0.1198 -0.1408 ...
#>   ..$ acceleration: num [1:747] -0.2207 -0.1792 -0.1393 -0.1017 -0.0669 ...
#>  $ survival_data    :'data.frame':	50 obs. of  6 variables:
#>   ..$ id    : int [1:50] 1 2 3 4 5 6 7 8 9 10 ...
#>   ..$ time  : num [1:50] 8.13 7.77 1.64 8.38 5.17 ...
#>   ..$ status: int [1:50] 0 0 1 0 1 1 0 1 1 0 ...
#>   ..$ w1    : num [1:50] 0.3219 -0.7838 1.5757 0.6429 0.0898 ...
#>   ..$ w2    : num [1:50] 1.201 1.045 -1.003 1.848 -0.667 ...
#>   ..$ b     : num [1:50] 0.1371 -0.0565 0.0363 0.0633 0.0404 ...

# Check data characteristics
cat("Event rate:", mean(sim$survival_data$status), "\n")
#> Event rate: 0.68 
cat(
  "Observations per subject:",
  nrow(sim$longitudinal_data) / nrow(sim$survival_data), "\n"
)
#> Observations per subject: 14.94 

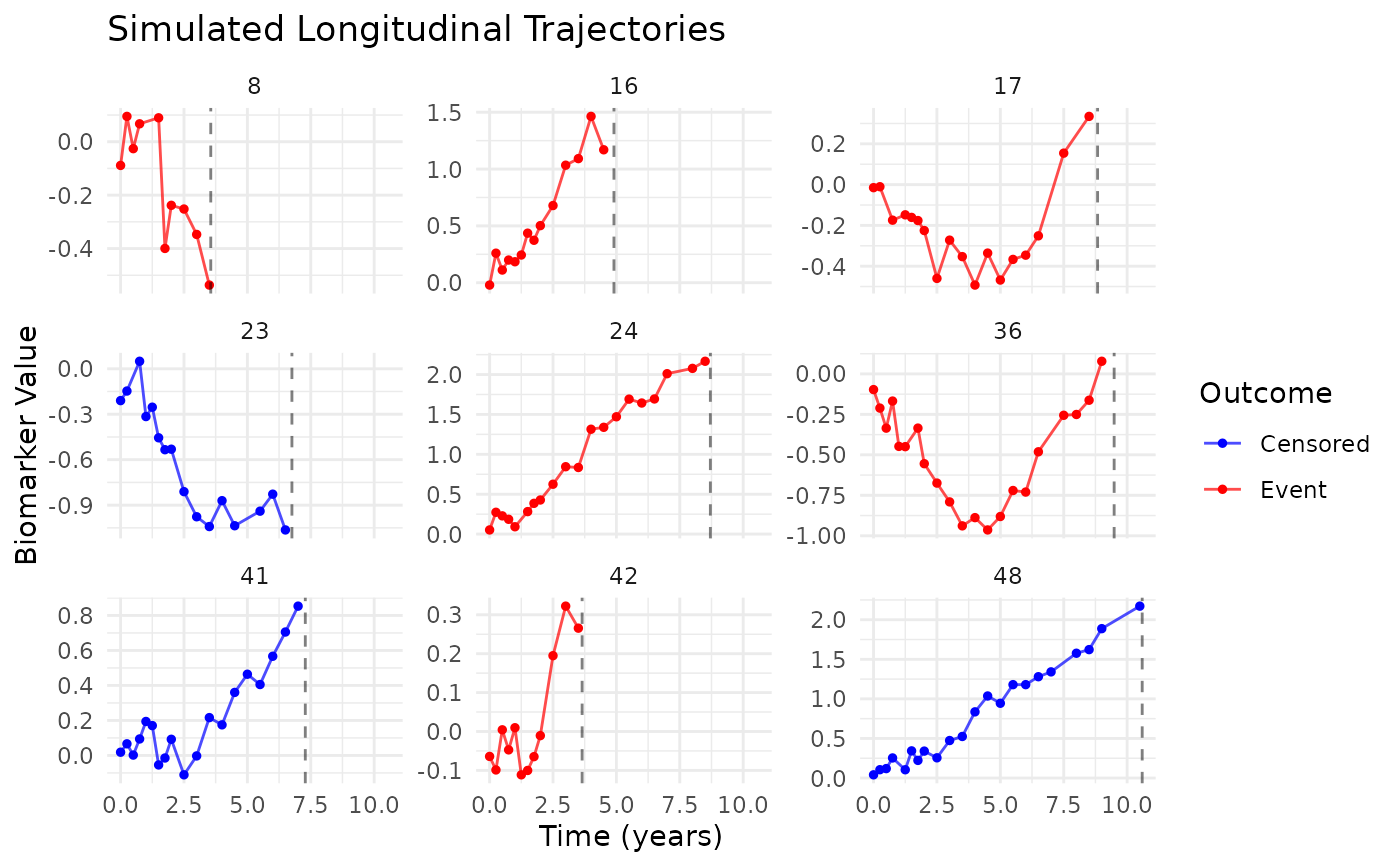
# Visualize trajectories with survival information
library(ggplot2)
library(dplyr)
#> 
#> Attaching package: ‘dplyr’
#> The following objects are masked from ‘package:stats’:
#> 
#>     filter, lag
#> The following objects are masked from ‘package:base’:
#> 
#>     intersect, setdiff, setequal, union

# Select subjects with different outcomes
plot_data <- sim$longitudinal_data %>%
  left_join(sim$survival_data[, c("id", "time", "status")],
    by = "id", suffix = c("", "_event")
  ) %>%
  filter(id %in% sample(unique(id), 9))

ggplot(plot_data, aes(x = time, y = v)) +
  geom_line(aes(color = factor(status)), alpha = 0.7) +
  geom_point(aes(color = factor(status)), size = 1) +
  geom_vline(aes(xintercept = time_event),
    linetype = "dashed", alpha = 0.5
  ) +
  facet_wrap(~id, scales = "free_y", ncol = 3) +
  scale_color_manual(
    values = c("0" = "blue", "1" = "red"), labels = c("Censored", "Event")
  ) +
  theme_minimal() +
  labs(
    x = "Time (years)", y = "Biomarker Value", color = "Outcome",
    title = "Simulated Longitudinal Trajectories"
  )